Différence entre la transposition et la transposition conjuguée
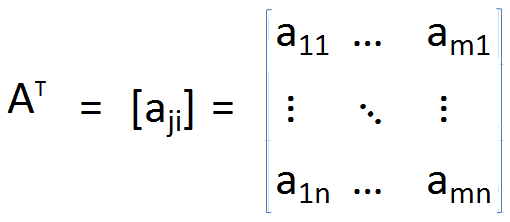
Transposition VS conjuguée Transpose
Transposer une matrice UN Peut être identifié comme la matrice obtenue en réorganisant les colonnes comme des lignes ou des lignes sous forme de colonnes. En conséquence, les indices de chaque élément sont interchangés. Plus formellement, transposer une matrice UN, est défini comme
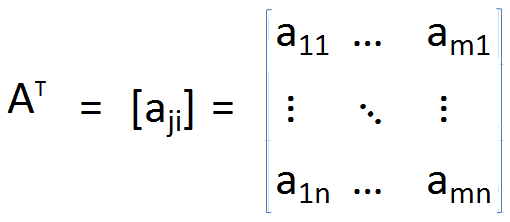
où
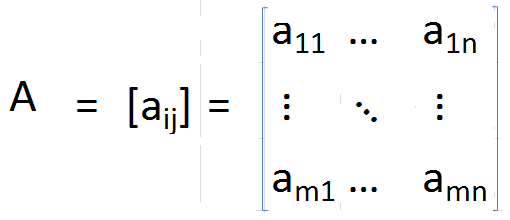
Dans une matrice de transport, la diagonale reste inchangée. Mais tous les autres éléments sont tournés autour de la diagonale. De plus, la taille des matrices passe également de m × n à n × m.
La transposition a des propriétés importantes, et ils permettent une manipulation plus facile des matrices. De plus, certaines matrices de transport importantes sont définies en fonction de leurs caractéristiques. Si la matrice est égale à sa transposition, alors la matrice est symétrique. Si la matrice est égale à son négatif de la transposition, alors la matrice est un biais symétrique.
La transposition conjuguée d'une matrice est la transposition de la matrice avec les éléments remplacés par son conjugué complexe. C'est-à-dire le conjugué complexe (UN*) est défini comme la transposition du conjugué complexe de la matrice UN.
UN*= (Ā)T; En détail,
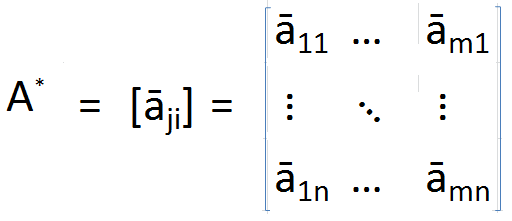
où
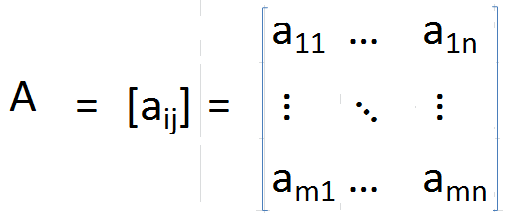
et àji ε C.
Il est également connu sous le nom de conjugué d'ermitien et de conjugué hermitien. Si la transposition conjuguée est égale à la matrice elle-même, la matrice est connue sous le nom de matrice hermitienne. Si la transposition conjuguée est égale au négatif de la matrice, c'est une matrice hérmitienne biaisée. Et si l'inverse de la matrice est égal au conjugué complexe, la matrice est unitaire.
De même, tous les conjugués complexes de matrices spéciales possèdent également des propriétés spéciales qui peuvent être utilisées pour les manipuler mathématiquement facilement. La transposition conjuguée est largement utilisée dans la mécanique quantique et ses champs pertinents.
Quelle est la différence entre la transposition et la transposition conjuguée?
• La transposition d'une matrice est obtenue en réorganisant les colonnes en rangées ou en lignes en colonnes. Le conjugué complexe d'une matrice est obtenu en remplaçant chaque élément par son conjugué complexe (i.e x + iy ⇛ x-iy ou vice versa). La transposition conjuguée est obtenue en effectuant les deux opérations sur la matrice.
• Par conséquent, la transposition conjuguée n'est qu'une matrice de transposition avec ses conjugués complexes comme éléments.


