Différence entre le parallélogramme et le losange

Parallélogramme vs rhombus
Le parallélogramme et le rhombon sont des quadrilatéraux. La géométrie de ces figures était connue de l'homme depuis des milliers d'années. Le sujet est explicitement traité dans le livre «Elements» écrit par le mathématicien grec Euclide.
Parallélogramme
Le parallélogramme peut être défini comme la figure géométrique avec quatre côtés, avec des côtés opposés parallèles les uns aux autres. Plus précisément, c'est un quadrilatère avec deux paires de côtés parallèles. Cette nature parallèle donne de nombreuses caractéristiques géométriques aux parallélogrammes.
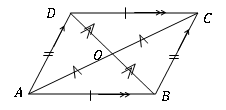
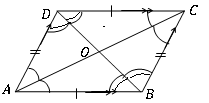
Un quadrilatère est un parallélogramme si des caractéristiques géométriques suivantes sont trouvées.
• Deux paires de côtés adverses sont égaux en longueur. (Ab = dc, ad = bc)
• Deux paires d'angles opposés sont de taille égale. ([latex] d \ hat a b = b \ hat c d, a \ hat d c = a \ hat b c [/ latex]))
• Si les angles adjacents sont supplémentaires [latex] d \ hat a b + a \ hat d c = a \ hat d c + b \ hat c d = b \ hat c d + A \ hat b c = a \ hat b c + d \ hat a b = 180 ^ \ circ = \ pi rad [/ latex]
• Une paire de côtés, qui s'opposent les uns les autres, est parallèle et égale en longueur. (Ab = dc & ab∥dc)
• Les diagonales se bissent (ao = oc, bo = od)
• Chaque diagonale divise le quadrilatère en deux triangles congruents. (∆Adb ≡ ∆Bcd, ∆Abc ≡ ∆Adc)
De plus, la somme des carrés des côtés est égale à la somme des carrés de diagonales. Ceci est parfois appelé loi parallélogramme et a des applications généralisées en physique et en ingénierie. (UN B2 + avant JC2 + CD2 + Da2 = AC2 + Bd2)
Chacune des caractéristiques ci-dessus peut être utilisée comme propriétés, une fois qu'il est établi que le quadrilatère est un parallélogramme.
La zone du parallélogramme peut être calculée par le produit de la longueur d'un côté et de la hauteur du côté opposé. Par conséquent, la zone du parallélogramme peut être indiquée comme
Zone du parallélogramme = base × hauteur = ab × h
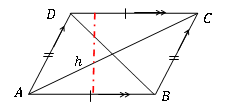
La zone du parallélogramme est indépendante de la forme du parallélogramme individuel. Il dépend uniquement de la longueur de la base et de la hauteur perpendiculaire.
Si les côtés d'un parallélogramme peuvent être représentés par deux vecteurs, la zone peut être obtenue par l'ampleur du produit vectoriel (produit transversal) des deux vecteurs adjacents.
Si les côtés AB et AD sont représentés par les vecteurs ([latex] \ revershArrow ab [/ latex]) et ([latex] \ reversightArrow ad [/ latex]) respectivement, la zone du parallélogramme est donnée par [ Latex] \ Left | \ reversightArrow ab \ Times \ reversightArrow ad \ droite | = Ab \ cdot ad \ sin \ alpha [/ latex], où α est l'angle entre [latex] \ revershArrow ab [/ latex] et [latex] \ reversharrow ad [/ latex].
Voici quelques propriétés avancées du parallélogramme;
• La zone d'un parallélogramme est le double de la zone d'un triangle créé par l'une de ses diagonales.
• La zone du parallélogramme est divisée en deux par n'importe quelle ligne passant par le milieu.
• Toute transformation affine non dégénérée porte un parallélogramme à un autre parallélogramme
• Un parallélogramme a une symétrie rotationnelle de l'ordre 2
• La somme des distances de tout point intérieur d'un parallélogramme sur les côtés est indépendante de l'emplacement du point
Rhombe
Un quadrilatère avec tous les côtés est égale en longueur est connu sous le nom de rhombus. Il est également nommé comme un quadrilatère équilatéral. Il est considéré comme ayant une forme de diamant, similaire à celui des cartes à jouer.
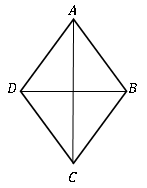
Le losange est également un cas particulier du parallélogramme. Il peut être considéré comme un parallélogramme avec les quatre côtés égaux. Et il a des propriétés spéciales suivantes, en plus des propriétés d'un parallélogramme.
• Les diagonales du rhombus se bissent à angle droit; Les diagonales sont perpendiculaires.
• Les diagonales bissent les deux angles internes opposés.
• Au moins deux des côtés adjacents sont égaux en longueur.
La zone du losange peut être calculée dans la même méthode que le parallélogramme.
Quelle est la différence entre le parallélogramme et le losange?
• Le parallélogramme et le losange sont des quadrilatoires. Le losange est un cas particulier des parallélogrammes.
• La zone de n'importe qui peut être calculée à l'aide de la base de formule × hauteur.
• Considérer les diagonales;
- Les diagonales du parallélogramme se bissettent, et bissettent le parallélogramme pour former deux triangles congrus.
- Les diagonales du rhombus se diminuent à angle droit et les triangles formés sont équilatéraux.
• Considérer les angles internes;
- Les angles internes opposés du parallélogramme sont de taille égale. Deux angles internes adjacents sont supplémentaires.
- Les angles internes du losange sont bissectés par les diagonales.
• Considérer les côtés;
- Dans un parallélogramme, la somme des carrés des côtés est égale à la somme des carrés de la diagonale (loi de parallélogramme).
- Comme les quatre côtés sont égaux dans un losange, quatre fois le carré d'un côté est égal à la somme des carrés de la diagonale.


