Différence entre radian et degré

Radian vs degré

Degrés et Radians sont des unités de mesure angulaire. Les deux sont couramment utilisés dans la pratique, dans des domaines tels que les mathématiques, la physique, l'ingénierie et de nombreuses autres sciences appliquées. Le diplôme a une histoire qui remonte à l'histoire babylonienne ancienne tandis que Radian est un concept mathématique relativement moderne introduit en 1714 par Roger Cotes.

Degré

Le degré est l'unité élémentaire la plus couramment utilisée de mesure angulaire. Même si c'est l'unité la plus courante en pratique, ce n'est pas l'unité SI de mesure angulaire.

Un diplôme (diplôme d'arc) est défini comme 1 / 360e de l'angle total d'un cercle. Il est en outre divisé en minutes (minutes d'arc) et secondes (secondes d'arc). Une minute d'arc est le 1 / 60e de degré, et un deuxième arc est 1 / 60e d'arc minute. Une autre méthode de subdivision est un degré décimal, où un degré d'arc est divisé en 100. Un centième de degré est connu et symbolisé par le terme diplômé.

Radian

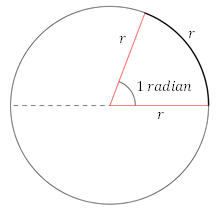
Un radian est défini comme l'angle plan sous-tendu par un arc circulaire de longueur qui est égal à son rayon.

Radian est l'unité standard de mesure angulaire, et elle est utilisée dans de nombreux domaines de mathématiques et ses applications. Radian est également une unité SI dérivée de mesure angulaire, et elle est sans dimension. Les radians sont symbolisés en utilisant le terme rad derrière les valeurs numériques.

Un cercle sous-tend un angle de 2π rad au centre et un demi-cercle sous-tend π rad. Un angle droit est π / 2 rad.

Ces relations permettent une conversion des degrés en radians et vice versa.

1^° = π / 180 rad ↔ 1 rad = 180 ° / π

Par rapport à d'autres unités, Radian est préféré en raison de sa nature naturelle. Lorsqu'il est appliqué, Radian permet plus d'interprétation en mathématiques que les autres unités. Sauf en géométrie pratique, en calcul, analyse et autres sous-disciplines des mathématiques Radian est utilisé.

Quelle est la différence entre les radians et les degrés?

• Un degré est une unité purement basée sur la quantité de rotation ou de virage tandis que Radian est basé sur la longueur de l'arc produit par chaque angle.

• Un degré est 1 / 360e de l'angle d'un cercle tandis que Radian est l'angle sous-tendu par un arc circulaire qui a la même longueur que son rayon. Il s'ensuit qu'un cercle sous-tend 3600 ou 2π radians.

• Les degrés sont divisés en minutes d'arc et des secondes d'arc, tandis que les radians n'ont pas de subdivision, mais utilisent des décimales pour les angles plus petits et les angles fractionnaires.

• Radian soutient l'interprétation plus facile des concepts en mathématiques; Par conséquent, permettre une application en physique et autres sciences pures (par exemple, considérez les définitions de la vitesse tangentielle).

• Les degrés et les radians sont des unités sans dimension.