Différence entre le groupe de points et le groupe spatial
Différence clé - groupe de points VS Espace Groupe
Le groupe de points des termes et le groupe spatial sont utilisés en cristallographie. La cristallographie est l'étude de la disposition des atomes dans un solide cristallin. Le groupe de points cristallographiques est un ensemble d'opérations de symétrie qui laissent au moins un point incessant. Une opération de symétrie est un acte d'obtention de l'image d'origine d'un objet même après l'avoir déplacé. Les opérations de symétrie utilisées dans les groupes de points sont des rotations et des réflexions. Un groupe spatial est le groupe de symétrie 3D d'une configuration dans l'espace. Un groupe de symétrie est le groupe de toutes les transformations obtenues sans varier la composition pendant l'opération de groupe. Le différence clé entre le groupe de points et le groupe spatial est que Il existe 32 groupes de points cristallographiques alors qu'il y a 230 groupes spatiaux créés par la combinaison de 32 groupes de points et 14 réseaux bravais.
CONTENU
1. Aperçu et différence clé
2. Qu'est-ce que le groupe de points
3. Qu'est-ce que le groupe spatial
4. Comparaison côte à côte - groupe de points vs groupe spatial sous forme tabulaire
5. Résumé
Qu'est-ce que le groupe de points?
Le groupe de points cristallographiques est un ensemble d'opérations de symétrie qui laissent au moins un point incessant. Les opérations de symétrie décrites dans les groupes de points sont des rotations et des réflexions. Dans les opérations de symétrie du groupe de points, un point central de l'objet est maintenu incessant (fixe) tout en déplaçant d'autres faces de l'objet aux positions des caractéristiques du même type. Là, les caractéristiques macroscopiques de l'objet doivent rester les mêmes avant et après l'opération de symétrie.
Pour tout objet donné, il existe un certain nombre d'opérations de symétrie possibles (avec des relations géométriques définies entre les opérations de symétrie). L'objet aurait la symétrie décrite par le groupe de points. Par conséquent, différents objets ayant des symétries ponctuelles différentes sont décrits par différents groupes de points.
Dans la notation des groupes ponctuels, il y a deux systèmes utilisés;
-
Notation de Schoenflies
Dans le système de notation Schoenflies, les groupes de points sont nommés CNV, CNH, DNH, Td, OH, etc. Les différents symboles utilisés dans ce système de notation sont donnés ci-dessous.
- n est le nombre le plus élevé d'axes de rotation
- v est le plan miroir vertical (mentionné uniquement lorsqu'il n'y a pas de plans miroir horizontaux)
- H est les plans miroir horizontaux
- T est un groupe de points tétraédriques
- est un groupe de points octaédrique
Par exemple, Cn est utilisé indique que le groupe ponctuel a un axe de rotation N fois. Quand il est donné comme CNH, Cela signifie qu'il y a un Cn avec un plan miroir (plan de réflexion) perpendiculaire à l'axe de rotation. En revanche, cNV est Cn avec un plan miroir parallèle à l'axe de rotation. Si le groupe de points est donné comme s2n, il indique que le groupe de points n'a qu'un axe de réflexion de rotation 2n fois.
-
Notation Hermann-Mauguin
Le système de notation Hermann-Mauguin est couramment utilisé pour les groupes spatiaux. Mais, il est également utilisé pour les groupes de points cristallographiques. Il donne l'axe de rotation le plus élevé. Par exemple, le groupe de points ayant seulement un axe de rotation 2 fois est indiqué comme 2. Le groupe de points donné comme c2h par schoenflies, la notation est donnée comme 2 / m dans le système de notation Hermann-Mauguin dans lequel le symbole «m» indique un plan miroir et le symbole de slash indique que le plan miroir est perpendiculaire à l'axe double. Le tableau suivant montre différentes notations de groupes de points pour différents systèmes de réseau.
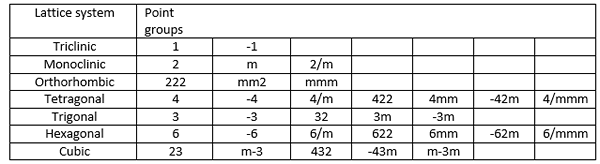

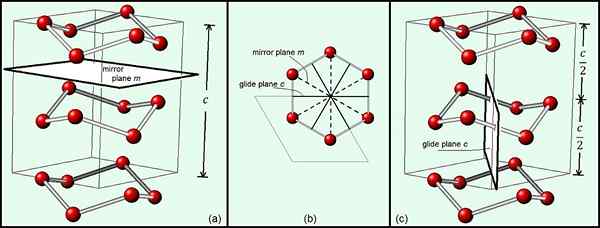
Figure 01: Les plans miroir et les plans de glissure de glace hexagonale indiquent que le groupe spatial de glace est p63 / mmc
Il y a 32 groupes de points. Les groupes de points les plus simples sont 1, 2, 3, 4, 5 et 6. Tous ces groupes de points ne comprennent qu'un seul axe de rotation. Pour les inversions rotatives, il y a des axes nommés -1, M, -3, -4 et -6. 22 autres groupes de points sont des combinaisons de ces groupes de points.
Qu'est-ce que le groupe spatial?
Un groupe spatial est le groupe de symétrie 3D d'une configuration dans l'espace. Il y a 230 groupes spatiaux. Ces 230 groupes sont une combinaison de 32 groupes de points cristallographiques (mentionnés ci-dessus) et 14 réseaux bravais. Le Bravais sont donnés dans le tableau ci-dessous.
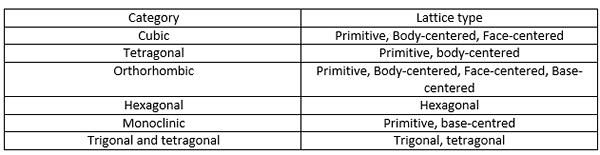
Un groupe spatial donne une description de la symétrie d'un cristal. Les groupes spatiaux sont des combinaisons de symétrie translationnelle des opérations de cellules unitaires et de symétrie telles que la rotation, l'inversion rotative, la réflexion, l'axe de vis et les opérations de symétrie plane de glide.
Quelle est la différence entre le groupe de points et le groupe spatial?
Groupe de points vs groupe spatial | |
| Le groupe de points cristallographiques est un ensemble d'opérations de symétrie qui laissent au moins un point incessant. | Un groupe spatial est le groupe de symétrie 3D d'une configuration dans l'espace. |
| Composants | |
| Il y a 32 groupes de points cristallographiques. | Il y a 230 groupes spatiaux (créés par la combinaison de 32 groupes de points et 14 réseaux Bravais). |
| Opérations de symétrie | |
| Les opérations de symétrie utilisées dans la détection du groupe de points sont la rotation et la réflexion. | Les opérations de symétrie utilisées dans la détection des groupes d'espace sont la rotation, l'inversion rotative, la réflexion, l'axe de vis et les opérations de symétrie du plan de glissement. |
Résumé - Groupe de points VS Espace Groupe
Les groupes de points et les groupes spatiaux sont des termes décrits sous cristallographie. Le groupe de points cristallographiques est un ensemble d'opérations de symétrie qui laissent tous au moins un point incessant. Un groupe spatial est le groupe de symétrie 3D d'une configuration dans l'espace. La différence entre le groupe de points et le groupe spatial est qu'il existe 32 groupes de points cristallographiques alors qu'il y a 230 groupes spatiaux (créés par la combinaison de 32 groupes de points et 14 réseaux bravais).
Référence:
1.«2: Éléments d'opérations de symétrie et de symétrie.”Chemistry LibreTexts, LibreTexts, 6 mai 2017. Disponible ici
2.«Groupe de points cristallographiques.»Wikipedia, Wikimedia Foundation, 28 février. 2018. Disponible ici
Image gracieuseté:
1.'Ice ih Space Group' par dbuckingham42 - propre travail, (cc by-sa 4.0) via Commons Wikimedia


