Différence entre le prisme triangulaire et la pyramide triangulaire (tétraèdre)

Prisme triangulaire vs pyramide triangulaire (tétraèdre)

En géométrie, un polyèdre est un solide géométrique en trois dimensions avec des faces plates et des bords droits. Un prisme est un polyèdre avec une base polygonale à z côté, une base identique sur un autre plan et aucun autre parallélogramme se joignant aux côtés correspondants des deux bases.

Une pyramide est un polyèdre formé en connectant une base polygonale et un point, connu sous le nom de l'apex. La base est un polygone et les côtés du polygone sont connectés à l'apex à travers des triangles.

Prisme triangulaire

Un prisme triangulaire est un prisme avec les triangles comme base; je.e. Les sections transversales du solide parallèle aux bases sont des triangles à tout moment dans le solide. Il peut également être considéré comme un pentaèdre avec deux des côtés parallèles les uns aux autres, tandis que la surface normale aux trois autres surfaces se trouve dans le même plan (un plan différent des plans de base). Les côtés autres que les bases sont toujours des rectangles.

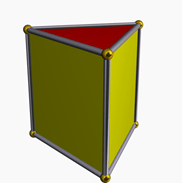
Le prisme est dit un prisme droit Si les plans des bases sont perpendiculaires aux autres surfaces.

Le volume du prisme est donné par

Volume = zone de base × hauteur

C'est le produit de la zone du triangle de base et la longueur entre les deux bases. 

Pyramide triangulaire (tétraèdre)

Une pyramide triangulaire est un objet solide composé de triangles dans les quatre côtés. C'est le type le plus simple des pyramides. Il est également connu sous le nom de tétraèdre, qui est également un type de polyèdres.

Il peut également être considéré comme un objet solide formé en rejoignant les lignes des sommets d'un triangle à un point au-dessus des triangles. Dans cette définition, les visages du tétraèdre peuvent être des triangles différents. Cependant, le cas souvent rencontré est le tétraèdre ordinaire, qui a des triangles équilatéraux comme ses côtés.

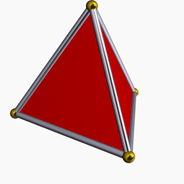
Le volume du tétraèdre peut être obtenu en utilisant la formule suivante.

Volume = (1/3) Zone de base × hauteur

Ici, la hauteur fait référence à la distance normale entre la base et l'apex.

Étant donné que sa figure se forme directement à partir des triangles, les tétraèdres affichent de nombreuses propriétés analogues des triangles, tels que Circnsphere, Insphere, Exspheres et Tetrahedron médial. Il possède des centres respectifs tels que Circumcenter, Incentiter, Excenters, Spieker Center et des points tels qu'un centroïde.

Quelle est la différence entre le prisme triangulaire et la pyramide triangulaire (tétraèdre)?

• Le prisme triangulaire et la pyramide triangulaire (tétraèdre) sont des polyhédrons, mais le prisme triangulaire se compose de triangles comme base du prisme avec.

• Par conséquent, le prisme triangulaire a 5 côtés, 6 sommets et 9 bords tandis que le tétraèdre a 4 côtés, 4 sommets et 6 bords.

• La zone de section transversale le long de l'axe à travers les bases ne change pas dans le prisme triangulaire, mais dans le tétraèdre, la zone de section transversale change (diminue avec la distance de la base) le long de l'axe perpendiculaire à la base.

• Si le tétraèdre et le prisme triangulaire ont le même triangle que la base et la même hauteur, le volume du prisme est trois fois le volume du tétraèdre.