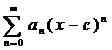Différence entre la série de puissance et la série Taylor

Série de puissance contre la série Taylor
En mathématiques, une véritable séquence est une liste ordonnée de nombres réels. Formellement, c'est une fonction de l'ensemble des nombres naturels à l'ensemble des nombres réels. Si unnest alorse terme d'une séquence, nous désignons la séquence par ou par un1, un2,… ,unn,… .Par exemple, considérez la séquence 1, ½, ⅓,… , 1/ /n,… . Il peut être indiqué 1 / n.
Il est possible de définir une série en utilisant des séquences. Une série est la somme des termes d'une séquence. Par conséquent, pour chaque séquence, il y a une séquence associée et vice-versa. Si unn est la séquence considérée, alors, la série formée par cette séquence peut être représentée comme:
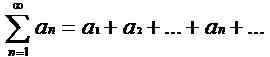
Ainsi, dans l'exemple ci-dessus, la série associée est 1+1/ /2+1/ /3+… + 1/ /n +… .
Comme les noms le suggèrent, la série Power est un type spécial de séries et il est largement utilisé dans l'analyse numérique et la modélisation mathématique connexe. La série Taylor est une série de puissance spéciale qui fournit une façon alternative et facile à manipuler de représenter des fonctions bien connues.
Qu'est-ce que la série Power?
Une série de puissance est une série de la forme
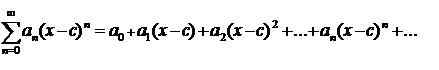
qui est convergent (éventuellement) pour un intervalle centré sur c. Les coefficients unn peut être des nombres réels ou complexes, et est indépendant de X; je.e. la variable factice.
Par exemple, en définissant unn= 1 pour chacun n, et c = 0, la série de puissance 1 + x + x2+… + Xn+… Est obtenu. Il est facile d'observer que lorsque x ε (-1,1), cette série de puissance converge vers 1 / (1-x).
Une série de puissance converge quand X = c. Les autres valeurs de X pour lequel la série Power Converges prendra toujours la forme d'un intervalle ouvert centré sur c. C'est, Il y aura une valeur 0≤ R ≤ ∞ tel que pour chacun X satisfaisant | x-c | ≤R, La série de puissance est convergente et pour chacun X satisfaisant | x-c |>R, La série Power est divergente. Cette valeur R est appelé rayon de convergence de la série de puissance (R peut prendre n'importe quelle valeur réelle ou infinité positive).
La série de puissance peut être ajoutée, soustraite, multipliée et divisée en utilisant les règles suivantes. Considérez les deux séries de puissance:
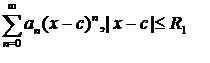
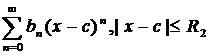 .
.
Alors,
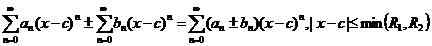
je.e. comme des termes sont ajoutés ou soustraits ensemble. De plus, il est possible de multiplier et de diviser les deux séries de puissance en utilisant l'identité,
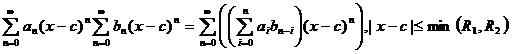
Qu'est-ce que la série Taylor?
La série Taylor est définie pour une fonction F(X) qui est infiniment différenciable sur un intervalle. Supposer F(X) est différenciable sur un intervalle centré sur c. Puis la série de puissance qui est donnée par
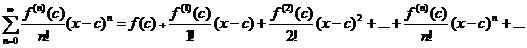
est appelé l'expansion de la série Taylor de la fonction F(X) à propos c. (Ici F(n)(c) Désigner le ne dérivé à X = c). Dans l'analyse numérique, un nombre fini de termes dans cette expansion infinie est utilisé pour calculer les valeurs aux points où la série est convergente vers la fonction d'origine.
Une fonction F(X) serait analytique dans l'intervalle (un B), si pour chaque x ε (a, b), la série taylor de F(X) converge vers la fonction F(X). Par exemple, 1 / (1-x) est analytique sur (-1,1), depuis son expansion de Taylor 1 + x + x2+… + Xn+… Converge vers la fonction sur cet intervalle, et eX est analytique partout, puisque la série Taylor eXconverge vers eX Pour chaque nombre réel X.
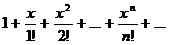
Quelle est la différence entre la série Power et la série Taylor?
1. La série Taylor est une classe spéciale de séries de puissance définies uniquement pour les fonctions qui sont infiniment différenciables sur un intervalle ouvert.
2. La série Taylor prend la forme spéciale
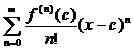
tandis qu'une série de puissance peut être n'importe quelle série de la forme