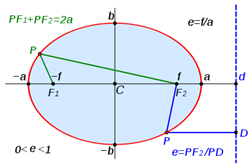
Différence entre l'hyperbole et l'ellipse
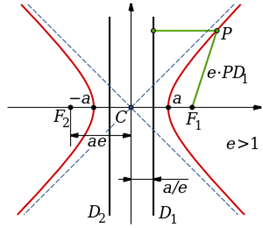
Hyperbole vs ellipse
Lorsqu'un cône est coupé à différents angles, différentes courbes sont marquées par le bord du cône. Ces courbes sont souvent appelées les sections coniques. Plus précisément, une section conique est une courbe obtenue en croisant une surface conique circulaire droite avec une surface plane. À différents angles d'intersection, différentes sections coniques sont données.
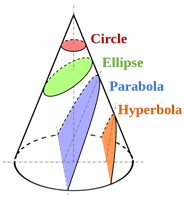
L'hyperbola et l'ellipse sont des sections coniques, et leurs différences sont facilement comparées dans ce contexte.
En savoir plus sur Ellipse
Lorsque l'intersection de la surface conique et de la surface plane produit une courbe fermée, elle est connue sous le nom d'ellipse. Il a une excentricité entre zéro et un (0 Le segment de ligne passant par les foyers est connu sous le nom d'axe majeur, et l'axe perpendiculaire à l'axe majeur et passant par le centre de l'ellipse est connu sous le nom d'axe mineur. Les diamètres le long de chaque axe sont connus comme le diamètre transversal et le diamètre conjugué respectivement. La moitié de l'axe majeur est connue sous le nom de l'axe semi-majeur, et la moitié de l'axe mineur est connu sous le nom de l'axe semi-minor. Chaque point F1 et f2 sont connus comme les foyers de l'ellipse et des longueurs F1 + PF2 = 2A , où P est un point arbitraire sur l'ellipse. Excentricité e est défini comme le rapport entre la distance entre une focalisation et le point arbitraire ( PF2 ) et la distance perpendiculaire au point arbitraire de la directive (PD). Il est également égal à la distance entre les deux foyers et l'axe semi-majeur: e = PF / PD = FA L'équation générale de l'ellipse, lorsque l'axe semi-majeur et l'axe semi-minor coïncident avec les axes cartésiens, est donné comme suit. X2/un2 + y2/ b2 = 1 La géométrie de l'ellipse a de nombreuses applications, en particulier en physique. Les orbites des planètes dans le système solaire sont elliptiques avec le soleil comme une orientation. Les réflecteurs pour les antennes et les dispositifs acoustiques sont fabriqués en forme elliptique pour profiter du fait que toute forme d'émission se concentrera sur l'autre focus. En savoir plus sur l'hyperbole L'hyperbole est également une section conique, mais elle est ouverte. Le terme hyperbola est référé aux deux courbes déconnectées illustrées sur la figure. Plutôt que de fermer comme une ellipse, les bras ou les branches de l'hyperbole continuent jusqu'à l'infini. Les points où les deux branches ont la distance la plus courte entre eux sont connus sous le nom de sommets. La ligne traversant les sommets est considérée comme le principal axe ou l'axe transversal, et c'est l'un des principaux axes de l'hyperbole. Les deux foyers de la parabole se trouvent également sur l'axe majeur. Le point médian de la ligne entre les deux sommets est le centre, et la longueur du segment de ligne est l'axe semi-majeur. La bissectrice perpendiculaire de l'axe semi-majeur est l'autre axe principal, et les deux courbes de l'hyperbole sont symétriques autour de cet axe. L'excentricité de la parabole est supérieure à un; e> 1. Si les axes principaux coïncisent avec les axes cartésiens, l'équation générale de l'hyperbole est de la forme: X2/un2 - y2/ b2 = 1, où un est l'axe semi-majeur et b est la distance entre le centre et l'une ou l'autre focalisation. Les hyperbolas avec des extrémités ouvertes face à l'axe X sont connues sous le nom d'hyperbolas est-ouest. Des hyperbolas similaires peuvent également être obtenus sur l'axe y. Ceux-ci sont connus sous le nom d'hyperbolas de l'axe y. L'équation de ces hyperbolas prend la forme y2/un2 - X2/ b2 = 1 Quelle est la différence entre l'hyperbole et l'ellipse? • Les ellipses et l'hyperbole sont des sections coniques, mais l'ellipse est une courbe fermée tandis que l'hyperbole se compose de deux courbes ouvertes. • Par conséquent, l'ellipse a un périmètre fini, mais l'hyperbole a une longueur infinie. • Les deux sont symétriques autour de leur axe majeur et mineur, mais la position de la directrice est différente dans chaque cas. Dans l'ellipse, il se trouve à l'extérieur de l'axe semi-majeur tandis que, dans l'hyperbole, il se trouve dans l'axe semi-majeur. • Les excentricités des deux sections coniques sont différentes. 0 eHyperbole > 0 • L'équation générale des deux courbes est la même, mais elles sont différentes. • La bissectrice perpendiculaire de l'axe majeur coupe la courbe dans l'ellipse, mais pas dans l'hyperbole. (Images Source: Wikipedia)