Différence entre point fixe et point d'équilibre

Le différence clé entre le point fixe et le point d'équilibre est que Le point fixe est utile pour trouver l'état d'équilibre d'un système, tandis que le point d'équilibre est l'état auquel le système ne change pas car les variables du système changentd.

Le point fixe et le point d'équilibre sont des termes utiles en mathématiques pour identifier l'état d'équilibre d'un système physique souhaité.

CONTENU

1. Aperçu et différence clé
2. Qu'est-ce que le point fixe 
3. Qu'est-ce que le point d'équilibre
4. Similitudes entre le point fixe et le point d'équilibre
5. Comparaison côte à côte - point fixe vs point d'équilibre dans la forme tabulaire
6. Résumé

Qu'est-ce que le point fixe?

Le point fixe d'une fonction en mathématiques est un élément du domaine de cette fonction qui peut être mappé à lui-même via la fonction. En d'autres termes, «c» est un point fixe de la fonction «f» lorsque f (c) = c. Ceci est également connu sous le nom de point fixe ou invariant. Par conséquent, f (f (… f (c)…)) = fⁿ(c) = c qui est une préoccupation de terminaison importante concernant l'informatique récursive «F». Nous pouvons nommer un ensemble de points fixes comme un ensemble fixe.

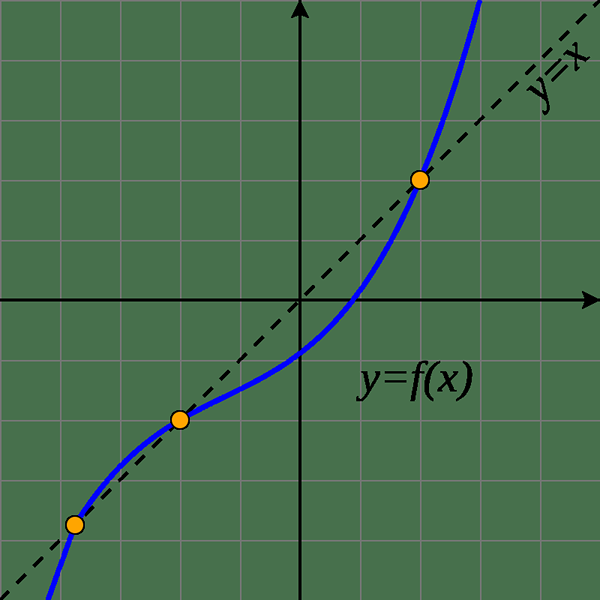
Considérons un exemple afin de comprendre ce phénomène. Si nous prenons «f» en nombre réel par f (x) = x² - 3x +4, alors 2 est un point fixe de «f» car f (2) = 2. Cependant, toutes les fonctions n'ont pas de points fixes. E.g. Lorsque f (x) = x + 1, il n'a pas de points fixes parce que «x» n'a jamais égal à «x +1» pour un nombre réel. Compte tenu de la terminologie graphique, un point fixe «x» fait référence au point (x, f (x)) qui est sur la ligne y = x. En d'autres termes, le graphique de «F» contient un point en commun avec cette ligne.

Les points fixes sont des points périodiques ayant leur période égale à un. Compte tenu de la géométrie projective, les points fixes d'une projectivité sont nommés en double point. Selon la théorie des Galois, la série de points fixes d'un ensemble d'automorphismes de terrain est nommé comme un champ fixe de cet ensemble d'automorphismes.

Il existe différentes applications de points fixes, notamment l'économie, la physique, les compilateurs de langage de programmation, la théorie des types, le vecteur sur les valeurs de pagerank de toutes les pages Web, la distribution stationnaire de la chaîne de Markov, etc.

Qu'est-ce que le point d'équilibre?

Un point d'équilibre est une solution constante à une équation différente en mathématiques. Ce terme vient principalement sous des équations différentielles en mathématiques. Nous pouvons classer les équilibres en observant les signes des valeurs propres de la linéarisation des équations sur les équilibres. En d'autres termes, nous pouvons classer les équilibres en évaluant la matrice jacobienne aux points d'équilibre du système souhaité, suivi par la recherche des valeurs propres qui en résultent. Là, nous pouvons déterminer le comportement du système dans le voisinage des points d'équilibre quantitativement en trouvant le ou les vecteurs propres qui sont associés aux valeurs propres.

On peut dire qu'un point d'équilibre est hyperbolique alors qu'aucune des valeurs propres n'a aucune partie réelle. Cependant, si toutes les valeurs propres ont une partie réelle négative, alors l'équilibre devient une équation stable. De même, s'il y a une partie réelle positive, alors l'équilibre devient instable. De plus, s'il y a au moins une partie réelle négative et au moins une partie réelle positive dans les valeurs propres, alors l'équilibre obtient un point de selle.

Quelles sont les similitudes entre le point fixe et le point d'équilibre?

• Ces points peuvent ne pas être stables.
• Les deux points sont décrits pour une condition en régime permanent d'un système.

Quelle est la différence entre le point fixe et le point d'équilibre?

Les termes point fixe et point d'équilibre sont utilisés en mathématiques. La principale différence entre le point fixe et le point d'équilibre est que le point fixe est utile pour trouver l'état d'équilibre d'un système, tandis que le point d'équilibre est l'état auquel le système ne change pas car les variables du système sont modifiées.

Résumé - point fixe vs point d'équilibre

Le point fixe et le point d'équilibre sont des termes utiles en mathématiques pour identifier l'état d'équilibre d'un système physique souhaité. La principale différence entre le point fixe et le point d'équilibre est que le point fixe est utile pour trouver l'état d'équilibre d'un système, tandis que le point d'équilibre est l'état auquel le système ne change pas car les variables du système sont modifiées.

Référence:

1. «Point fixe (mathématiques)." Wikipédia, Fondation Wikimedia, 26 mars. 2021, disponible ici.

Image gracieuseté:

1. «Exemple de point fixe» de Krishnavedala - Propre travaux (CC0) via Commons Wikimedia