Différence entre le diamant, le rhombus et le trapézoïde

Diamant, rhombus vs trapézoïde
 

Le diamant, le rhombus et le trapèze sont tous quadrilatères, qui sont des polygones à quatre côtés. Alors que le losange et le trapèze sont correctement définis en mathématiques, le diamant (ou forme de diamant) est un terme profane pour le losange.

Rhombus et diamant

Un quadrilatère avec tous les côtés égaux sont en longueur est connu sous le nom de rhombus. Il est également nommé comme un quadrilatère équilatéral. Il est considéré comme ayant une forme de diamant, similaire à celui des cartes à jouer. La forme du diamant n'est pas une entité géométrique définie avec précision.

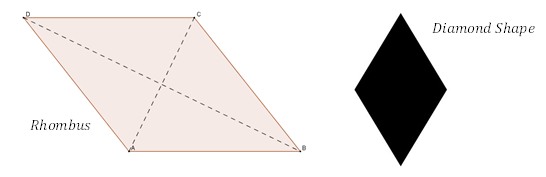
Le losange est un cas particulier du parallélogramme. Il peut être considéré comme un parallélogramme avec des côtés égaux. Le carré peut être considéré comme un cas particulier du losange, où les angles internes sont angles droits. En général, un losange a les propriétés spéciales suivantes

• Les quatre côtés sont égaux en longueur. (Ab = dc = ad = bc)

• Les diagonales du rhombus se bissent à angle droit; Les diagonales sont perpendiculaires les unes aux autres,

en plus des propriétés suivantes d'un parallélogramme.

• Deux paires d'angles opposés sont de taille égale. (Dâb = bĉd, un ̂DC = A ̂AVANT JC)

• Les angles adjacents sont complémentaires dâb + a ̂DC = A ̂DC + B ̂CD = B ̂CD + A ̂BC = A ̂BC + D ̂Ab = 180 ° = π rad

• Une paire de côtés, qui s'opposent les uns les autres, est parallèle et égal en longueur. (Ab = dc & ab∥dc)

• Les diagonales se bissent (ao = oc, bo = od)

• Chaque diagonale divise le quadrilatère en deux triangles congruents. (∆ADB ≡ ∆BCD, ∆ABC ≡ ∆ADC)

• Les diagonales bissent les deux angles internes opposés.

La zone du losange peut être calculée en utilisant la formule suivante.

Zone du rhombus = ½ (AC × BD)

Trapézoïde (trapèze)

Le trapézoïde est un quadrillatéral convexe où au moins deux côtés sont parallèles et inégaux de longueur. Les côtés parallèles du trapèzoïde sont connus sous le nom de bases et les deux autres côtés sont appelés le jambes.

Voici les principales caractéristiques des trapézoïdes;

• Si les angles adjacents ne sont pas sur la même base du trapézoïde, ce sont des angles supplémentaires. je.e. Ils ajoutent jusqu'à 180 ° (ba ̂d + ad ̂c = ab ̂c + bc ̂d = 180 °)

• Les deux diagonales du trapèze se croisent au même rapport (le rapport entre la section des diagonales est égal).

• Si A et B sont des bases et C, D sont des jambes, les longueurs des diagonales sont donnés par 

La zone du trapèze peut être calculée en utilisant la formule suivante.

Lis le Différence entre le parallélogramme et le trapézoïde

Quelle est la différence entre le diamant, le rhombus et le trapézoïde?

• Le rhombus et le trapèze sont des objets mathématiques bien définis tandis que la forme du diamant est un terme profane. Chaque forme a quatre côtés et la forme du diamant fait référence à un losange.

• Rhombus a des côtés égaux, avec des côtés opposés parallèles les uns aux autres. Le trapézoïde a des côtés inégaux en général, avec deux côtés parallèles les uns aux autres. Seules les jambes du trapèze peuvent être égales.

• Toute diagonale du losange sépare le losange en deux triangles congruents. Les triangles formés par les diagonales du trapézoïde ne sont pas nécessairement congrus.

• Les diagonales du losange se croisent à angle droit tandis que les diagonales du trapèzoïde ne sont pas nécessairement perpendiculaires.

• Les diagonales du rhombus se diminuent tandis que les diagonales du rhombus se croisent au même rapport.