Différence entre congruent et égal

Congruent vs égal

Les concepts congruents et égaux sont des concepts similaires en géométrie, mais souvent mal utilisés et confus.

Égal

Signifie égal que les amplitudes ou tailles de deux en comparaison sont les mêmes. Le concept d'égalité est un concept familier dans notre vie quotidienne; Cependant, en tant que concept mathématique, il doit être défini à l'aide de mesures plus strictes. Différents champs utilisent une définition différente de l'égalité. Dans la logique mathématique, il est défini à l'aide des axiomes de Paeno. L'égalité fait référence aux chiffres; souvent des nombres représentant des propriétés.

Dans le contexte de la géométrie, l'égalité a les mêmes implications que dans l'usage commun du terme égal. Il dit que si les attributs de deux figures géométriques sont les mêmes, les deux figures sont égales. Par exemple, la zone d'un triangle peut être égale à la zone d'un carré. Ici, seule la taille de la «zone» de la propriété est concernée, et ils sont les mêmes. Mais les chiffres eux-mêmes ne peuvent pas être considérés comme les mêmes. 

Conforme

Dans le contexte de la géométrie, des moyens congruents égaux à la fois dans les figures (forme) et les tailles. Ou en mots plus simples, si l'on peut être considéré comme une copie exacte de l'autre, les objets sont congruents, indépendamment du positionnement. C'est le concept équivalent d'égalité utilisé en géométrie. Dans le cas de la congruence, des définitions beaucoup plus strictes sont également fournies en géométrie analytique. 

Indépendamment de l'orientation des triangles qui sont ci-dessus, ils peuvent être positionnés pour qu'ils se chevauchent parfaitement. Par conséquent, ils sont égaux en taille et en forme. Ce sont donc des triangles congruents. Une figure et son image miroir sont également congruents. (Ils peuvent être chevauchés après les faire tourner autour d'un axe situé dans le plan de la forme). 

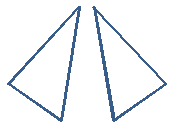
Dans ce qui précède, même si les figures sont des images miroir, elles sont congruents.

La congruence dans les triangles est importante dans l'étude de la géométrie plane. Pour que deux triangles soient congruents, les angles correspondants et les côtés doivent être égaux. Les triangles peuvent être considérés comme congruents si les conditions suivantes sont remplies.

• SSS (côté latéral)  Si les trois côtés correspondants sont égaux en longueur.

• SAS (côté d'angle latéral)  Une paire de côtés correspondants et l'angle inclus sont égaux.

• ASA (angle d'angle d'angle)  Une paire d'angles correspondants et le côté inclus sont égaux.

• AAS (côté angle d'angle)  Une paire d'angles correspondants et un côté non inclus sont égaux.

• HS (jambe d'hypoténuse d'un triangle droit)  Deux triangles droits sont congruents si l'hypoténuse et un côté sont égaux.

Le cas AAA (angle d'angle d'angle) n'est pas un cas où la congruence est toujours valable. Par exemple, les deux triangles ont des angles égaux, mais pas congruents parce que les tailles des côtés sont différentes. 

Quelle est la différence entre congruente et égal?

• Si certains attributs des chiffres géométriques sont les mêmes en amplitude, alors ils seraient égaux.

• Si les tailles et les chiffres sont égaux, alors les chiffres seraient congruents.

• L'égalité concerne l'ampleur (nombres) tandis que la congruence concerne à la fois la forme et la taille d'une figure.