Différence entre la distribution binomiale et normale

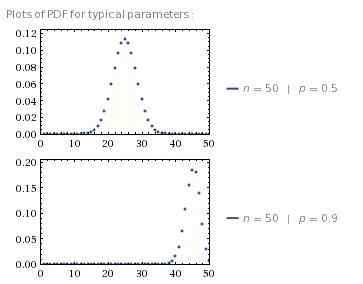
Distribution binomiale vs normale
 

Les distributions de probabilité de variables aléatoires jouent un rôle important dans le domaine des statistiques. Parmi ces distributions de probabilité, la distribution binomiale et la distribution normale sont deux des plus courantes dans la vie réelle.

Qu'est-ce que la distribution binomiale?

La distribution binomiale est la distribution de probabilité correspondant à la variable aléatoire X, qui est le nombre de succès d'un séquence finie des expériences Yes / non indépendantes dont chacune a une probabilité de succès p. De la définition de X, Il est évident qu'il s'agit d'une variable aléatoire discrète; Par conséquent, la distribution binomiale est également discrète.

La distribution est désignée comme X ~B(n,p) où n Le nombre d'expériences est-il la probabilité de succès. Selon la théorie des probabilités, nous pouvons déduire que B(n,p) suit la fonction de masse de probabilité [latex] b (n, p) \\ sim \\ binom n k p ^ k (1-p) ^ (n-k), k = 0, 1, 2,… n [/ latex]. De cette équation, on peut en outre déduire que la valeur attendue de X, E (X) = NP et la variance de X, V (X) = NP(1-p).

Par exemple, considérez une expérience aléatoire de lancer une pièce 3 fois. Définir le succès comme obtenant H, défaillance comme obtenant T et la variable aléatoire X comme le nombre de succès dans l'expérience. Alors X~B(3, 0.5) et la fonction de masse de probabilité de X donné par [latex] \\ binom 3 k 0.5 ^ k (0.5) ^ (3-k), k = 0, 1, 2.[/latex]. Par conséquent, la probabilité d'obtenir au moins 2 h est p (X ≥ 2) = P (X = 2 ou X = 3) = P (X = 2) + p (X = 3) = ³C₂(0.5²) (0.5¹) + ³C₃(0.5³) (0.5⁰) = 0.375 + 0.125 = 0.5.

Qu'est-ce que la distribution normale?

La distribution normale est la distribution de probabilité continue définie par la fonction de densité de probabilité, [latex] n (\\ mu, \\ sigma) \\ sim \\ frac 1 \\ sqrt 2 \\ pi \\ Sigma ^ 2 \\ e ^ - \\ frac (x - \\ mu) ^ 2 2 \\ Sigma ^ 2 [/ latex]. Les paramètres [latex] \\ mu et \\ sigma [/ latex] désignent la moyenne et l'écart type de la population d'intérêt. Lorsque [latex] \\ mu = 0 et \\ sigma = 1 [/ latex], la distribution est appelée distribution normale standard.

Cette distribution est appelée normale car la plupart des phénomènes naturels suivent la distribution normale. Car, par exemple, le QI de la population humaine est normalement distribué. Comme le montre le graphique, il est unimodal, symétrique sur la moyenne et la forme de la cloche. La moyenne, le mode et la médiane coïncidaient. La zone sous la courbe correspond à la partie de la population, satisfaisant à une condition donnée.

Les parties de la population dans l'intervalle [latex] (\\ mu - \\ sigma, \\ mu + \\ sigma) [/ latex], [latex] (\\ mu - 2 \\ sigma, \\ mu + 2 \\ sigma) [/ latex], [latex] (\\ mu - 3 \\ sigma, \\ mu + 3 \\ sigma) [/ latex] sont environ 68.2%, 95.6% et 99.8% respectivement.

Quelle est la différence entre les distributions binomiales et normales?

• La distribution binomiale est une distribution de probabilité discrète tandis que la distribution normale est continue.
• La fonction de masse de probabilité de la distribution binomiale est [latex] b (n, p) \\ sim \\ binom n k p ^ k (1-p) ^ (n-k) [/ latex] , tandis que la fonction de densité de probabilité de la distribution normale est [latex] n (\\ mu, \\ sigma) \\ sim \\ frac 1 \\ sqrt 2 \\ pi \\ Sigma ^ 2 \\ e ^ - \\ frac (x - \\ mu) ^ 2 2 \\ Sigma ^ 2 [/ latex]
• La distribution binomiale est approximée avec une distribution normale dans certaines conditions mais pas l'inverse.