Différence entre la transposition et la matrice inverse

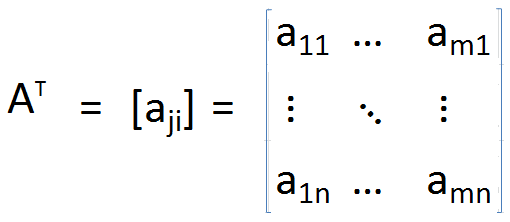
Transposer Vs Matrice inverse
 

La transposition et l'inverse sont deux types de matrices avec des propriétés spéciales que nous rencontrons en algèbre matricielle. Ils sont différents les uns des autres et ne partagent pas une relation étroite car les opérations effectuées pour les obtenir sont différentes.

Ils ont de larges applications dans le domaine de l'algèbre linéaire et les implémentations dérivées telles que l'informatique.

En savoir plus sur la matrice de transposition

Transposer une matrice UN Peut être identifié comme la matrice obtenue en réorganisant les colonnes comme des lignes ou des lignes sous forme de colonnes. En conséquence, les indices de chaque élément sont interchangés. Plus formellement, transposition de matrice UN, est défini comme

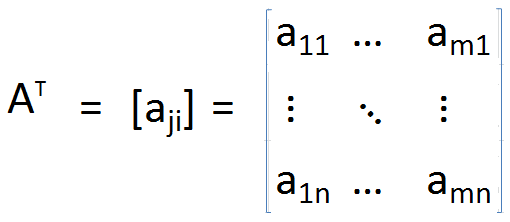
où

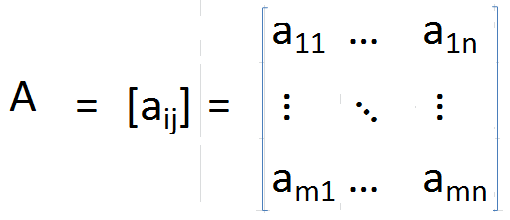
Dans une matrice de transport, la diagonale reste inchangée, mais tous les autres éléments sont tournés autour de la diagonale. De plus, la taille des matrices passe également de m × n à n × m.

La transposition a des propriétés importantes, et ils permettent une manipulation plus facile des matrices. De plus, certaines matrices de transport importantes sont définies en fonction de leurs caractéristiques. Si la matrice est égale à sa transposition, alors la matrice est symétrique. Si la matrice est égale à son négatif de la transposition, la matrice est un biais symétrique. La transposition conjuguée d'une matrice est la transposition de la matrice avec les éléments remplacés par son conjugué complexe.

En savoir plus sur la matrice inverse

L'inverse d'une matrice est défini comme une matrice qui donne la matrice d'identité lorsqu'elle est multipliée ensemble. Par conséquent, par définition, si Ab = ba = i alors B est la matrice inverse de UN et UN est la matrice inverse de B. Donc, si nous considérons B = UN^-1 , alors AA^-1 = UN^-1A = i

Pour qu'une matrice soit inversible, la condition nécessaire et suffisante est que le déterminant de UN n'est pas zéro; je.E |UN| = DET (UN) ≠ 0. Une matrice est censée être inversible, non singulaire ou non dégénérative si elle satisfait cette condition. Il suit que UN est une matrice carrée et les deux UN^-1 et UN a la même taille.

L'inverse de la matrice UN Peut être calculé par de nombreuses méthodes en algèbre linéaire telles que l'élimination gaussienne, la composition eigenge, la décomposition de Cholesky et la règle de Carmer. Une matrice peut également être inversée par la méthode d'inversion de blocs et la série Neuman.

Quelle est la différence entre la transposition et la matrice inverse?

• La transposition est obtenue en réorganisant les colonnes et les rangées dans la matrice tandis que l'inverse est obtenu par un calcul numérique relativement difficile. (Mais en réalité, les deux sont des transformations linéaires)

• En conséquence directe, les éléments de la transposition ne changent que leur position, mais les valeurs sont les mêmes. Mais dans l'inverse, les nombres peuvent être complètement différents de la matrice d'origine.

• Chaque matrice peut avoir une transposition, mais l'inverse est défini uniquement pour les matrices carrées, et le déterminant doit être un déterminant non nul.