Différence entre l'accélération tangentielle et l'accélération centripète

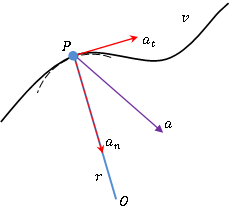
Accélération tangentielle vs accélération centripète

L'accélération est le taux de changement de vitesse, et lorsqu'il est exprimé en utilisant le calcul, c'est la dérivée temporelle de la vitesse. L'accélération tangentielle et l'accélération centripète sont des composantes de l'accélération pour une particule ou un corps rigide dans un mouvement circulaire.

Accélération tangentielle

Considérez une particule se déplaçant le long d'un chemin comme indiqué dans le diagramme. À l'instance considérée, la particule est en mouvement angulaire, et la vitesse de la particule est tangentielle sur le chemin.

Le taux de variation de la vitesse tangentielle est défini comme l'accélération tangentielle, et il est désigné par un_t.

un_t = DV_t/ dt

Cependant, cela ne tient pas compte de l'accélération totale de la particule. Selon la première loi de Newton, pour qu'une particule s'écarte du chemin et du virage rectiligne, il doit y avoir une autre force; Nous pouvons donc déduire qu'il doit y avoir une composante d'accélération dirigée perpendiculaire à la composante d'accélération tangentielle, i.e. vers le point O à l'instance montrée. Cette composante d'accélération est connue sous le nom de accélération normale, Et il est indiqué par un_n.

un_n = V_t²/ r

Si u_t et u_n sont les vecteurs unitaires dans les directions tangentielles et normales, l'accélération résultante peut être donnée par l'expression suivante.

a = a_tu_t + un_nu_n = (dv_t/ dt) u_t + (V_t²/ r) u_n

Accélération centripète

Considérez maintenant que la force induisant l'accélération normale est constante. Dans ce cas, la particule entre un chemin circulaire avec un rayon R. Il s'agit d'un cas particulier dans le mouvement angulaire, et l'accélération normale reçoit le terme accélération centripète. La force qui stimule le mouvement circulaire est connue sous le nom de force centripète.

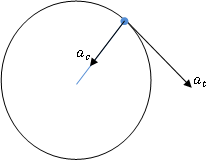
L'accélération centripète est également donnée par l'expression ci-dessus, mais les relations angulaires dans la vitesse et l'accélération peuvent être utilisées pour lui donner en termes de vitesse angulaire.

Donc,

un_c = V_t²/ r = -rΩ²

(Le signe négatif indique que l'accélération pointée dans la direction opposée du vecteur de rayon)

L'accélération nette peut être obtenue par le résultat des deux composants a_c et un_t.

Quelle est la différence entre l'accélération tangentielle et l'accélération centripète?

• Les accélérations tangentielles et centripète sont deux composantes de l'accélération d'une particule / corps dans un mouvement circulaire.

• L'accélération tangentielle est le taux de changement de vitesse tangentielle, et elle est toujours tangentielle sur le chemin circulaire, et normal au vecteur de rayon.

• L'accélération centripète est pointée vers le centre du cercle, et cette composante d'accélération est le facteur majeur qui maintient la particule dans le chemin circulaire.

• Pour une particule dans un mouvement circulaire, le vecteur d'accélération se trouve toujours dans le chemin circulaire.