Différence entre la relation et la fonction

Fonction Relation vs
 

À partir des mathématiques du secondaire, la fonction devient un terme commun. Même s'il est utilisé assez souvent, il est utilisé sans compréhension appropriée de sa définition et de ses interprétations. Cet article se concentre sur la description de ces aspects d'une fonction.

Relation

Une relation est un lien entre les éléments de deux ensembles. Dans un cadre plus formel, il peut être décrit comme un sous-ensemble du produit cartésien de deux ensembles x et y. Le produit cartésien de x et y, désigné X × Y, est un ensemble de paires ordonnées composées d'éléments des deux ensembles, souvent désignés (x, y). Les ensembles ne doivent pas être différents. Par exemple, un sous-ensemble d'éléments d'un × a, est appelé une relation sur un.

Fonction

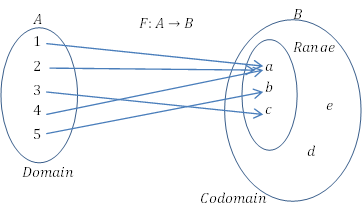
Les fonctions sont un type spécial de relations. Ce type spécial de relation décrit comment un élément est mappé à un autre élément d'un autre ensemble ou du même ensemble. Pour que la relation soit une fonction, deux exigences spécifiques doivent être satisfaites.

Chaque élément de l'ensemble où chaque mappage commence doit avoir un élément associé / lié dans l'autre ensemble.

Les éléments de l'ensemble où commence la cartographie ne peut être associé / lié à un et un seul élément de l'autre ensemble

L'ensemble à partir de laquelle la relation est mappée est connue sous le nom de domaine. L'ensemble, où la relation est mappée est connue sous le nom de codomaine. Le sous-ensemble d'éléments dans le codomaine ne contenant que les éléments liés à la relation est connu sous le nom de gamme.

Techniquement, une fonction est une relation entre deux ensembles, où chaque élément d'un ensemble est mappé de manière unique sur un élément de l'autre.

 Remarquez ce qui suit

• Chaque élément du domaine est mappé dans le codomaine.
• Plusieurs éléments du domaine sont connectés à la même valeur dans le codomaine, mais un seul élément du domaine ne peut pas être connecté à plus d'un élément du codomaine. (La cartographie doit être unique)
• Si chaque élément du domaine est mappé en éléments distincts et uniques dans le codomaine, la fonction serait une fonction «un à un».

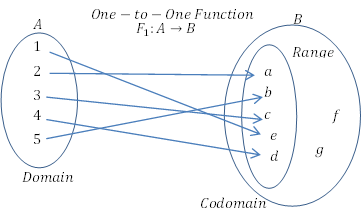
• Le codomaine contient un élément autre que ceux connectés aux éléments du domaine. La gamme n'a pas besoin d'être le codomaine. Si le codomaine est égal à la plage, la fonction est connue sous le nom de fonction «sur».

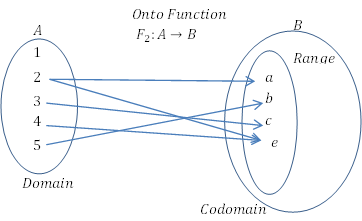
Lorsque les valeurs qui peuvent être prises par la fonction sont réelles, elle est appelée une fonction réelle. Les éléments du codomaine et du domaine sont des nombres réels.

Les fonctions sont toujours désignées à l'aide de variables. Les éléments du codomaine sont symboliquement représentés par la variable. La notation f (x) représente les éléments de la gamme. La relation peut être représentée en utilisant l'expression sous la forme f (x) = x ^ 2. Il dit que l'élément du domaine est mappé dans le carré de l'élément, dans le codomaine. 

Quelle est la différence entre la fonction et la relation?

• Les fonctions sont un type spécial de relations.

• La relation est basée sur le produit cartésien de deux ensembles.

• La fonction est basée sur des relations avec des propriétés spécifiques.

• Le domaine d'une fonction doit être mappé dans le codomaine de telle sorte que chaque élément ait une valeur correspondante et déterminée de manière unique dans le codomaine. La relation peut lier un seul élément à plusieurs valeurs.