Différence entre la parabole et l'hyperbole
Parabole vs hyperbola
Kepler a décrit les orbites des planètes comme des ellipses qui ont ensuite été modifiées par Newton car il a montré que ces orbites étaient des sections coniques spéciales telles que la parabole et l'hyperbole. Il existe de nombreuses similitudes entre une parabole et une hyperbole, mais il existe également des différences car il existe différentes équations pour résoudre des problèmes géométriques impliquant ces sections coniques. Pour mieux comprendre les différences entre une parabole et une hyperbole, nous devons comprendre ces sections coniques.

Image gracieuseté: http: // cseligman.com
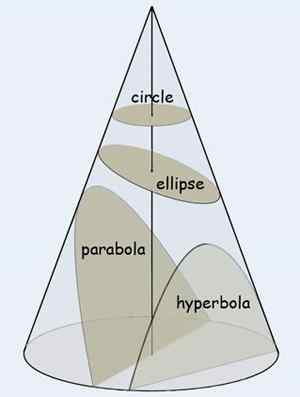
Une section est une surface ou le contour de cette surface formée en coupant une figure solide avec un plan. Si la figure solide se trouve être un cône, la courbe résultante est appelée une section conique. Le type et la forme de la section conique sont déterminés par l'angle d'intersection du plan et l'axe du cône. Lorsque le cône est coupé à angle droit à l'axe, nous obtenons une forme circulaire. Lorsqu'il est coupé à moins d'un angle droit, mais plus que l'angle fait par le côté du cône entraîne une ellipse. Lorsqu'il est coupé parallèle au côté du cône, la courbe obtenue est une parabole et lorsqu'elle est coupée presque parallèle à l'axe qui sur le côté, nous obtenons une courbe connue sous le nom d'hyperbole. Comme vous pouvez le voir sur les figures, les cercles et les ellipses sont des courbes fermées tandis que les parabolas et les hyperbolas sont des courbes ouvertes. Dans le cas d'une parabole, les deux bras finissent par être parallèles les uns aux autres alors que dans le cas d'une hyperbola, il n'est pas ainsi.
Étant donné que les cercles et les parabolas sont formés en coupant un cône à des angles spécifiques, tous les cercles sont de forme identique et que tous les parabolas sont de forme identique. Dans le cas des hyperbolas et des ellipses, il existe une large gamme d'angles entre le plan et l'axe, c'est pourquoi ils ont tendance à avoir une large gamme de formes. Les équations des quatre types de sections coniques sont les suivantes.
Cercle- x2+y2= 1
Ellipse- x2/un2+ y2/ b2= 1
Parabole2= 4ax
Hyperbola- x2/un2- y2/ b2= 1


