Différence entre les équations différentielles linéaires et non linéaires

Équations différentielles linéaires vs non linéaires
Une équation contenant au moins un coefficient différentiel ou une dérivée d'une variable inconnue est connue comme une équation différentielle. Une équation différentielle peut être linéaire ou non linéaire. La portée de cet article est d'expliquer ce qu'est l'équation différentielle linéaire, quelle est l'équation différentielle non linéaire et quelle est la différence entre les équations différentielles linéaires et non linéaires.
Depuis le développement du calcul au XVIIIe siècle par les mathématiciens comme Newton et Leibnitz, l'équation différentielle a joué un rôle important dans l'histoire des mathématiques. Les équations différentielles sont d'une grande importance en mathématiques en raison de leur gamme d'applications. Les équations différentielles sont au cœur de chaque modèle que nous développons pour expliquer tout scénario ou événement dans le monde, que ce soit en physique, ingénierie, chimie, statistiques, analyse financière ou biologie (la liste est sans fin). En fait, jusqu'à ce que le calcul devienne une théorie établie, les outils mathématiques appropriés n'étaient pas disponibles pour analyser les problèmes intéressants dans la nature.
Les équations résultantes à partir d'une application spécifique du calcul peuvent être très complexes et parfois non résolubles. Cependant, il y en a que nous pouvons résoudre, mais peut se ressembler et déroutant. Par conséquent, pour une identification plus facile, les équations différentielles sont classées par leur comportement mathématique. Linéaire et non linéaire est une telle catégorisation. Il est important d'identifier la différence entre les équations différentielles linéaires et non linéaires.
Qu'est-ce qu'une équation différentielle linéaire?
Supposer que F: X → Y et f (x) = y, a Équation différentielle sans termes non linéaires de la fonction inconnue y et ses dérivés sont connus comme une équation différentielle linéaire.
Il impose la condition que y ne peut pas avoir des termes d'index plus élevés tels que y2, y3,… Et des multiples de dérivés tels que
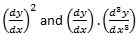
Il ne peut pas non plus contenir de termes non linéaires tels que le péché y, ey^ -2, ou LN y. Il prend la forme,
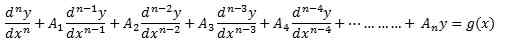
où y et g sont des fonctions de X. L'équation est une équation différentielle d'ordre n, qui est l'indice du dérivé d'ordre le plus élevé.
Dans une équation différentielle linéaire, l'opérateur différentiel est un opérateur linéaire et les solutions forment un espace vectoriel. À la suite de la nature linéaire de l'ensemble de solutions, une combinaison linéaire des solutions est également une solution à l'équation différentielle. C'est-à-dire si y1 et y2 sont des solutions de l'équation différentielle, alors C1 y1+ C2 y2 est aussi une solution.
La linéarité de l'équation n'est qu'un paramètre de la classification, et elle peut être classée en outre en équations différentielles homogènes ou non homogènes et ordinaires ou partielles. Si la fonction est g= 0 alors l'équation est une équation différentielle homogène linéaire. Si F est fonction de deux variables indépendantes ou plus (f: x, t → y) et f (x, t) = y , alors l'équation est une équation différentielle partielle linéaire.
La méthode de solution pour l'équation différentielle dépend du type et des coefficients de l'équation différentielle. Le cas le plus simple survient lorsque les coefficients sont constants. L'exemple classique de cette affaire est la deuxième loi du mouvement de Newton et ses diverses applications. La deuxième loi de Newton produit une équation différentielle linéaire de second ordre avec des coefficients constants.
Qu'est-ce qu'une équation différentielle non linéaire?
Les équations qui contiennent des termes non linéaires sont appelées équations différentielles non linéaires.
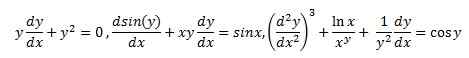
Tous ci-dessus sont des équations différentielles non linéaires. Les équations différentielles non linéaires sont difficiles à résoudre, par conséquent, une étude étroite est nécessaire pour obtenir une solution correcte. En cas d'équations différentielles partielles, la plupart des équations n'ont aucune solution générale. Par conséquent, chaque équation doit être traitée indépendamment.
L'équation de Navier-Stokes et l'équation d'Euler dans la dynamique des fluides, les équations sur le terrain d'Einstein de la relativité générale sont des équations différentielles partielles non linéaires bien connues. Parfois, l'application de l'équation de Lagrange à un système variable peut entraîner un système d'équations différentielles partielles non linéaires.
Quelle est la différence entre les équations différentielles linéaires et non linéaires?
• Une équation différentielle, qui n'a que les termes linéaires de la variable inconnue ou dépendante et de ses dérivés, est connue sous le nom d'équation différentielle linéaire. Il n'a pas de terme avec la variable dépendante de l'index supérieur à 1 et ne contient aucun de ses dérivés. Il ne peut pas avoir de fonctions non linéaires telles que les fonctions trigonométriques, la fonction exponentielle et les fonctions logarithmiques par rapport à la variable dépendante. Toute équation différentielle qui contient des termes mentionnés ci-dessus est une équation différentielle non linéaire.
• Les solutions d'équations différentielles linéaires créent un espace vectoriel et l'opérateur différentiel est également un opérateur linéaire dans l'espace vectoriel.
• Les solutions d'équations différentielles linéaires sont relativement plus faciles et des solutions générales existent. Pour les équations non linéaires, dans la plupart des cas, la solution générale n'existe pas et la solution peut être spécifique au problème. Cela rend la solution beaucoup plus difficile que les équations linéaires.


