Différence entre l'ISING et le modèle Heisenberg

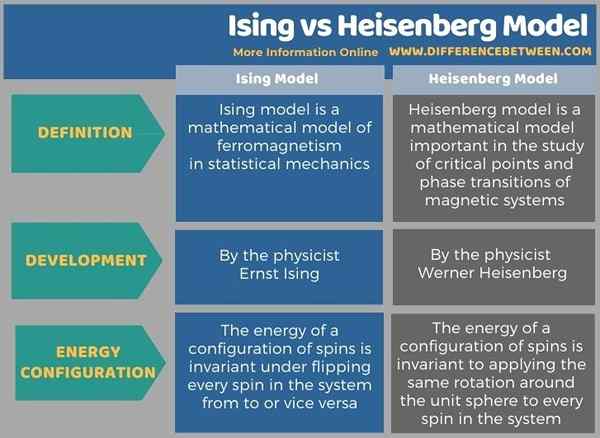
Le différence clé Entre Ising et le modèle Heisenberg est que Dans le modèle ISING, l'énergie d'une configuration de spins est invariante sous le retournement de chaque rotation du système de vers ou vice versa, tandis que dans le modèle de Heisenberg, l'énergie d'une configuration de spins est invariante à l'application de la même rotation autour de l'unité sphère à chaque tour du système.

Le modèle ISING a été développé et a été nommé d'après le physicien Ernst Ising. Le modèle de Heisenberg a été développé par Werner Heisenberg, un célèbre physicien.

CONTENU

1. Aperçu et différence clé
2. Qu'est-ce que le modèle Ising
3. Qu'est-ce que le modèle Heisenberg
4. Comparaison côte à côte - Ising vs heisenberg modèle sous forme tabulaire
5. Résumé

Qu'est-ce que le modèle Ising?

Le modèle ISING est un modèle mathématique de ferromagnétisme en mécanique statistique. Il a été nommé d'après le physicien Ernst Ising. Il existe des variables discrètes dans ce modèle représentant les moments dipolaires magnétiques des «spins» atomiques qui peuvent se produire dans l'un des deux états, +1 et -1. Dans ce modèle, nous organisons généralement les tours dans un réseau pour permettre à chaque rotation d'interagir avec ses voisins. Ce modèle nous permet d'identifier les transitions de phase comme un modèle de réalité simplifié. Le modèle ISING est l'un des modèles statistiques les plus simples pour montrer une transition de phase.

Lorsque l'on considère l'histoire de ce modèle, il a été inventé par le physicien Wilhelm Lenz en 1920. Il a donné ce modèle en tant que problème à son élève; Ernst Ising en 1925 où il a résolu le modèle. Mais sa solution n'a eu aucune transition de phase dedans. Le modèle de réseau carré bidimensionnel est très difficile qui a reçu une description analytique de Lars Onsager en 1944. Habituellement, ce modèle est résolu en utilisant la méthode de la matrice de transfert, bien qu'il existe également différentes approches existantes. Lorsque le nombre de dimensions est supérieur à quatre, la transition de phase du modèle ISING peut être décrite par la «théorie moyenne des champs».

Qu'est-ce que le modèle Heisenberg?

Le modèle Heisenberg est un modèle mathématique en physique statistique et est important dans l'étude des points critiques et des transitions de phase des systèmes magnétiques. Dans ce modèle, nous traitons les tours des systèmes magnétiques, quantique. Ce modèle a été développé par Werner Heisenberg, un célèbre physicien. Ce modèle est lié au modèle d'Ising prototypique.

Figure 01: Heisenberg, W. et Wigner, e

En mécanique quantique, le couplage dominant entre deux dipôles peut entraîner la plus basse énergie lorsqu'elles sont alignées. En prenant cela comme une hypothèse, nous pouvons développer des formules mathématiques pour le modèle Heisenberg.

Il existe des applications importantes du modèle Heisenberg. Il fournit un exemple théorique important et tractable pour appliquer la renormalisation de la matrice de densité. Nous pouvons résoudre le modèle à six vertex en utilisant la chaîne de spin Heisenberg. De plus, le modèle Hubbard à moitié rempli peut être cartographié sur un modèle Heisenberg avec une constante de couplage qui est inférieure à 0, représentant la force de l'interaction super-échange.

Quelle est la différence entre l'ising et le modèle Heisenberg?

Le modèle Ising et le modèle Heisenberg sont discutés principalement sous la physique statistique. La principale différence entre ISING et le modèle Heisenberg est que dans le modèle ISING, l'énergie d'une configuration de spins est invariante sous le renversement de chaque rotation du système de ou vice versa alors que dans le modèle de Heisenberg, l'énergie d'une configuration de spins est invariant à appliquer la même rotation autour de la sphère unitaire à chaque rotation du système.

Vous trouverez ci-dessous un résumé de la différence entre ISING et le modèle Heisenberg sous forme tabulaire.

Résumé - Ising vs Heisenberg Model

Le modèle ISING a été développé et a été nommé d'après le physicien Ernst Ising tandis que le modèle Heisenberg a été développé par Werner Heisenberg. La principale différence entre ISING et le modèle Heisenberg est que dans le modèle ISING, l'énergie d'une configuration de spins est invariante sous le renversement de chaque rotation du système de ou vice versa alors que dans le modèle de Heisenberg, l'énergie d'une configuration de spins est invariant à appliquer la même rotation autour de la sphère unitaire à chaque rotation du système.

Référence:

1. «Modèle Ising." Modèle d'Ising - un aperçu | Sujets ScienceDirect, Disponible ici.

Image gracieuseté:

1. «Heisenberg, W. Wigner, E. 1928 ”par Gfhund - Propre travaux (CC par 3.0) via Commons Wikimedia