Différence entre les expressions algébriques et les équations

Expressions algébriques vs équations
L'algèbre est l'une des principales branches des mathématiques et définit certaines des opérations fondamentales contribuant à la compréhension humaine des mathématiques, telles que l'addition, la soustraction, la multiplication et la division. L'algèbre introduit également le concept de variables, qui permet à une quantité inconnue d'être représentée par une seule lettre, d'où la commodité de la manipulation dans les applications.
En savoir plus sur les expressions algébriques
Un concept ou une idée peut être exprimé mathématiquement en utilisant les outils de base disponibles dans l'algèbre. Une telle expression est connue comme une expression algébrique. Ces expressions se composent de nombres, de variables et de différentes opérations algébriques.
Par exemple, considérez la déclaration «pour former le mélange, ajoutez 5 tasses de x et 6 tasses de y». Il est raisonnable d'exprimer le mélange comme 5x + 6y. Nous ne savons pas quoi ni combien sont X et Y, mais cela donne les mesures relatives dans le mélange. L'expression a du sens, mais pas du sens complet mathématiquement. x / y, x2+y, xy + xc sont tous des exemples d'expressions.
Pour plus de facilité d'utilisation, l'algèbre introduit sa propre terminologie pour les expressions.
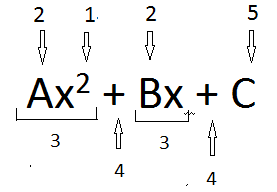
1. L'exposant 2. Coefficients 3. Trimestre 4. Opérateur algébrique 5. Une constante
N.B: Une constante peut également être utilisée comme coefficient.
Aussi, lors de l'exécution des opérations algébriques (E.g. Lors de la simplification d'une expression), la priorité de l'opérateur doit être suivie. La priorité de l'opérateur (priorité) dans l'ordre descendant est la suivante;
Supports
De
Division
Multiplication
Ajout
Soustraction
Cet ordre est communément connu par le mnémonique formé par les premières lettres de chaque opération, qui est Bodmas.
Historiquement, l'expression et les opérations algébriques ont apporté une révolution en mathématiques parce que la formulation de concepts mathématiques était plus facile, il en va de même pour les dérivations ou conclusions suivantes. Avant ce formulaire, les problèmes ont été principalement résolus en utilisant des ratios.
En savoir plus sur l'équation algébrique
Une équation algébrique est formée en reliant deux expressions à l'aide d'un opérateur d'affectation désignant l'égalité des deux parties. Il donne que le côté gauche est égal au côté droit. Par exemple, x2-2x + 1 = 0 et x / y-4 = 3x2+y sont des équations algébriques.
Habituellement, les conditions d'égalité ne sont satisfaites que pour certaines valeurs des variables. Ces valeurs sont connues comme les solutions de l'équation. Lorsqu'ils sont substitués, ces valeurs épuisent les expressions.
Si une équation se compose de polynômes des deux côtés, l'équation est connue comme une équation polynomiale. De plus, si une seule variable est dans l'équation, elle est connue comme une équation univariée. Pour deux variables ou plus, l'équation est appelée équations multivariées.
Quelle est la différence entre les expressions algébriques et les équations?
• L'expression algébrique est une combinaison de variables, constantes et opérateurs de telle sorte qu'ils forment ou plus pour donner un sens partiel des relations entre chaque variable. Mais les variables peuvent assumer toute valeur disponible dans son domaine.
• Une équation est de deux expressions ou plus avec une condition d'égalité et l'équation est vraie pour une ou plusieurs valeurs des variables. Une équation a un sens total tant que la condition d'égalité n'est pas violée.
• Une expression peut être évaluée pour des valeurs données.
• Une équation peut être résolue pour trouver une quantité ou une variable inconnue, en raison du fait ci-dessus. Les valeurs sont connues comme la solution à l'équation.
• L'équation porte un signe égal (=) dans l'équation.


